The area under the receiver operating characteristic (AUROC) is a performance metric that you can use to evaluate classification models. AUROC tells you whether your model is able to correctly rank examples:
- For a clinical risk prediction model, the AUROC tells you the probability that a randomly selected patient who experienced an event will have a higher predicted risk score than a randomly selected patient who did not experience an event (ref).
- For a binary handwritten digit classification model (“1” vs. “0”), the AUROC tells you the probability that a randomly selected “1” image will have a higher predicted probability of being a “1” than a randomly selected “0” image
AUROC is thus a performance metric for “discrimination”: it tells you about the model’s ability to discriminate between cases (positive examples) and non-cases (negative examples.) An AUROC of 0.8 means that the model has good discriminatory ability: 80% of the time, the model will correctly assign a higher absolute risk to a randomly selected patient with an event than to a randomly selected patient without an event.
How to interpret AUROC (ref)
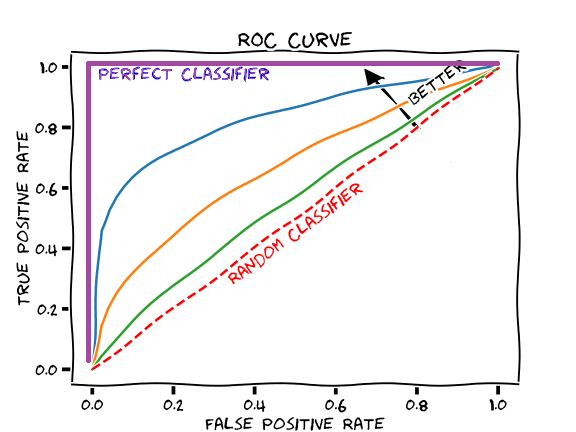
Figure: ROC Curves (modified from this cartoon)
The figure above shows some example ROC curves. The AUROC for a given curve is simply the area beneath it.
The worst AUROC is 0.5, and the best AUROC is 1.0.
- An AUROC of 0.5 (area under the red dashed line in the figure above) corresponds to a coin flip, i.e. a useless model.
- An AUROC less than 0.7 is sub-optimal performance
- An AUROC of 0.70 – 0.80 is good performance
- An AUROC greater than 0.8 is excellent performance
- An AUROC of 1.0 (area under the purple line in the figure above) corresponds to a perfect classifier
How to calculate AUROC
The AUROC is calculated as the area under the ROC curve. A ROC curve shows the trade-off between true positive rate (TPR) and false positive rate (FPR) across different decision thresholds. For a review of TPRs, FPRs, and decision thresholds, see Measuring Performance: The Confusion Matrix.
In plotted ROC curves (e.g. the figure of the previous section), the decision thresholds are implicit. The decision thresholds are not shown as an axis. The AUROC itself is also not explicitly shown; it is implied, as the area beneath the displayed ROC curve.
The x-axis of a ROC curve is the false positive rate, and the y-axis of a ROC curve is the true positive rate.
- A ROC curve always starts at the lower left-hand corner, i.e. the point (FPR = 0, TPR = 0) which corresponds to a decision threshold of 1 (where every example is classified as negative, because all predicted probabilities are less than 1.)
- A ROC curve always ends at the upper right-hand corner, i.e. the point (FPR = 1, TPR = 1) which corresponds to a decision threshold of 0 (where every example is classified as positive, because all predicted probabilities are greater than 0.)
- The points in between, which create the curve, are obtained by calculating the TPR and FPR for different decision thresholds between 1 and 0. For a rough, angular “curve”, you would use only a few decision thresholds: e.g. decision thresholds of [1, 0.75, 0.5, 0.25, 0]. For a smoother curve, you would use many decision thresholds, e.g. decision thresholds of [1, 0.98, 0.96, 0.94,…,0.08, 0.06, 0.04, 0.02, 0].
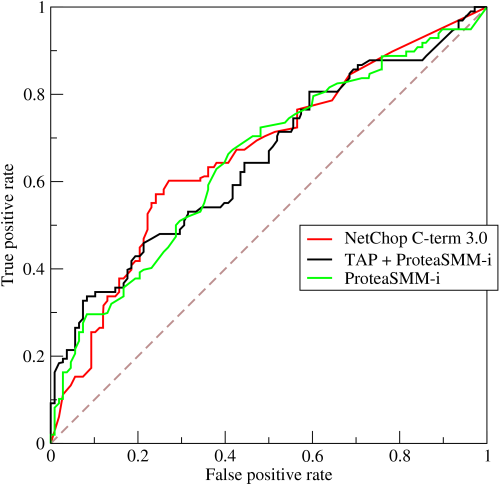
In the following figure, which shows ROC curves calculated on real data, the use of discrete decision thresholds is easier to appreciate in the jagged nature of the ROC curves:
Steps for calculating test set AUROC for a binary classification task:
- Train your machine learning model
- Use the trained model to make predictions on your test set, so that each example in your test set has a classification probability between 0 and 1.
- Using the model’s output predicted probabilities for the test set, calculate the TPR and FPR for different decision thresholds, and plot a ROC curve.
- Calculate the area under the ROC curve.
In practice, you don’t need to write code to calculate the AUROC manually. There are functions for calculating AUROC available in many programming languages. For example, in Python, you can do the following:
import sklearn.metrics
fpr, tpr, thresholds = sklearn.metrics.roc_curve(y_true = true_labels, y_score = pred_probs, pos_label = 1) #positive class is 1; negative class is 0
auroc = sklearn.metrics.auc(fpr, tpr)
First, you provide to the function sklearn.metrics.roc_curve() the ground truth test set labels as the vector y_true and your model’s predicted probabilities as the vector y_score, to obtain the outputs fpr, tpr, and thresholds. fpr is a vector with the calculated false positive rate for different thresholds; tpr is a vector with the calculated true positive rate for different thresholds; thresholds is a vector with the actual threshold values, and is just provided in case you’d like to inspect it (you don’t need the explicit thresholds vector in the next function.) The vectors fpr and tpr define the ROC curve. You then pass the fpr and tpr vectors to sklearn.metrics.auc() to obtain the AUROC final value.
When to use AUROC
The AUROC is more informative than accuracy for imbalanced data. It is a very commonly-reported performance metric, and it is easy to calculate using various software packages, so it is often a good idea to calculate AUROC for models that perform binary classification tasks.
It is also important to be aware of the limitations of AUROC. The AUROC can be “excessively optimistic” about the performance of models that are built for data sets with a much larger number of negative examples than positive examples. Many real-world data sets fit this description: for example, you would expect that in a data set drawn from the general population, there are many more healthy people (“negative for sickness”) than diseased people (“positive for sickness.”) In these cases, where true negatives dominate true positives, it may be difficult to use AUROC to distinguish the performance of two algorithms.
Why? In cases with many more negative examples than positive examples, a big improvement in the number of false positives only leads to a small change in the false positive rate. This is because false positive rate is calculated as false positives / (false positives + true negatives) and if we have a HUGE number of true negatives in the denominator, it’s going to be really hard to change the false positive rate only by changing the false positives.
Pretend Algorithm 1 has far fewer false positives than Algorithm 2 (i.e. Algorithm 1 is better). If the data has a lot of true negatives, the false positive rates of Algorithm 1 and Algorithm 2 are not going to be that different, and their AUROCs may not be that different.
Key takeaway: AUROC is a useful metric, but you should be aware that AUROC does not capture the effect of a large number of negative examples on an algorithm’s performance. An alternative performance metric that will not be “swamped” by true negatives is area under the precision-recall curve (AUPRC), which will be discussed in a future post.
Reference for this section (and a great resource for additional in-depth discussion): The Relationship Between Precision-Recall and ROC Curves
What if my model predicts more than two classes?
You can calculate the AUROC for each class separately, e.g. pretend that your task is composed of many different binary classification tasks: Class A vs. Not Class A, Class B vs. Not Class B, Class C vs. Not Class C…etc.
Nomenclature
The most common abbreviation for the area under the receiver operating characteristic is just “AUC.” This is poor terminology, as AUC just stands for “area under the curve” (and doesn’t specify what curve; the ROC curve is merely implied). Hence, in this post, I’ve preferred the abbreviation AUROC. You may also see the AUROC referred to as the c-statistic or “concordance statistic.”

The picture above shows an “auroch” , not to be confused with an “AUROC” :). The auroch is a now-extinct species of cattle that used to live in North Africa, Europe, and Asia. (Nature trivia brought to you by another member of Duke +DS who reminded me of aurochs in a discussion of the “AUROC” abbreviation.)
The end! Stay tuned for a future post about AUROC’s cousin, the AUPRC.

Comments are closed.